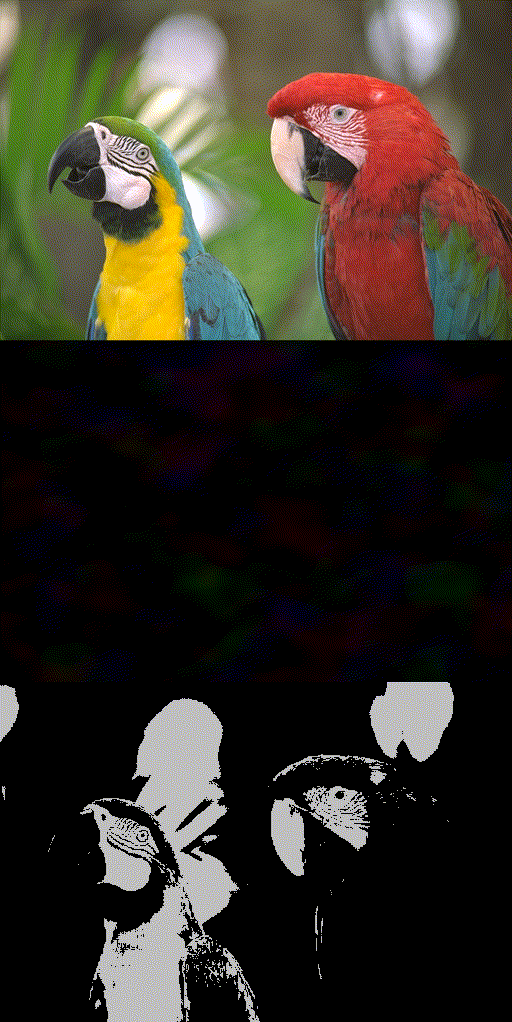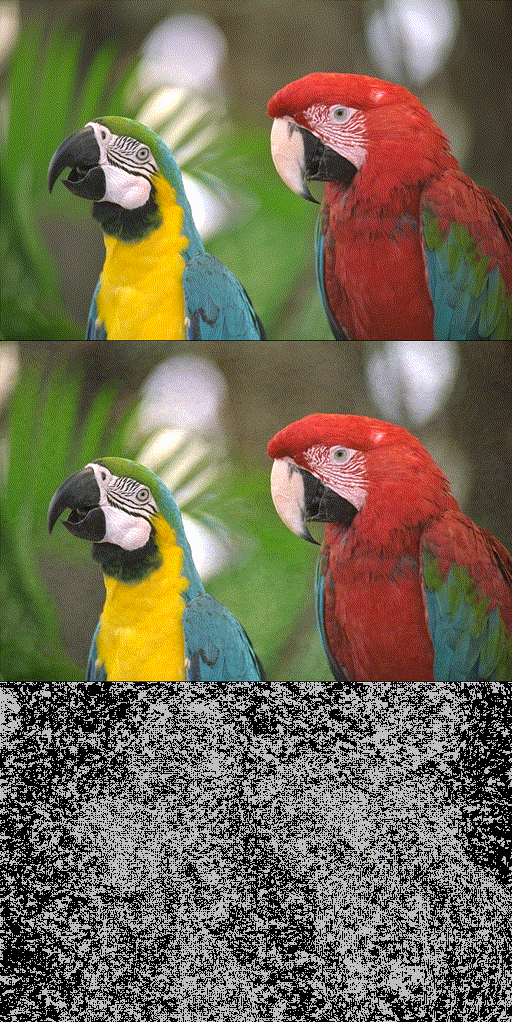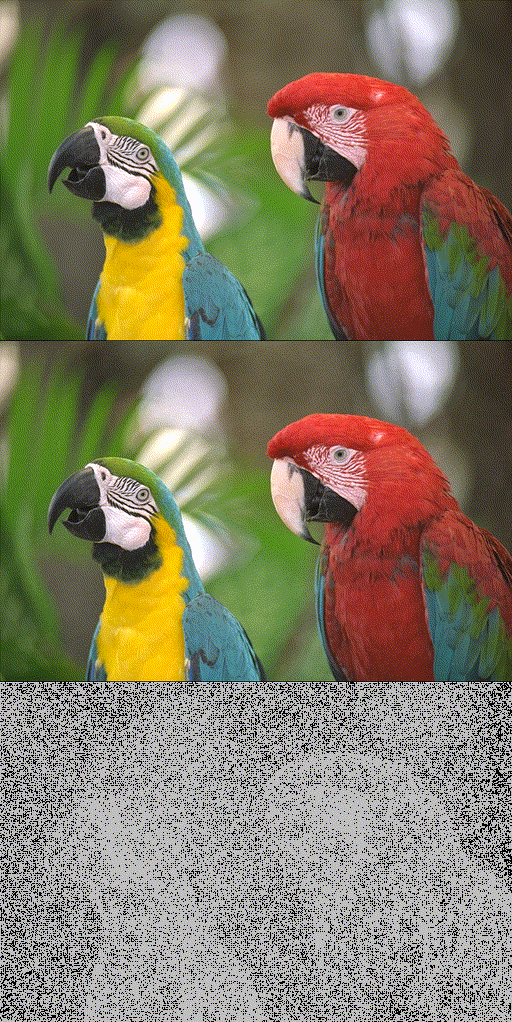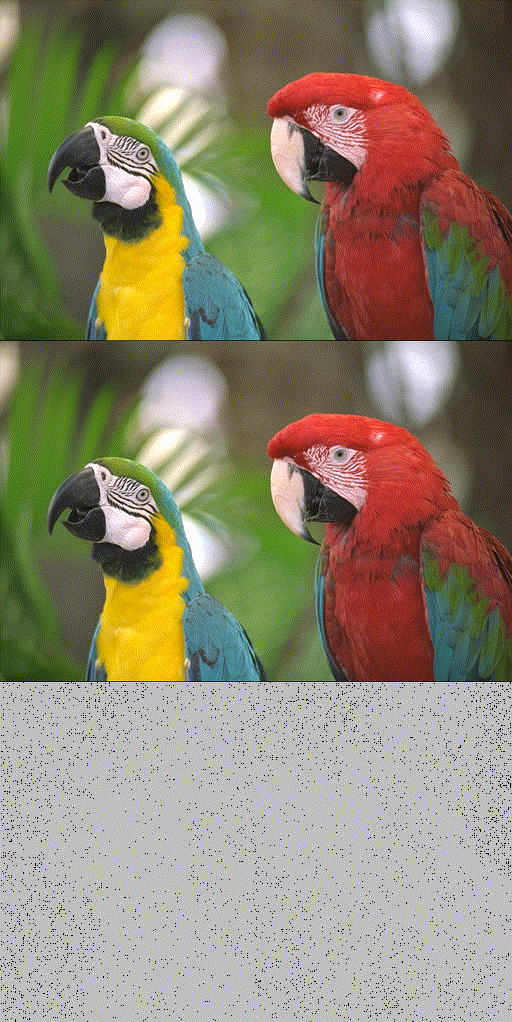Nonparametric Teaching of Implicit Neural Representations ICML 2024
- Chen Zhang* HKU
- Steven Tin Sui Luo* UoT
- Jason Chun Lok Li HKU
- Yik-Chung Wu HKU
- Ngai Wong HKU
Abstract
We investigate the learning of implicit neural representation (INR) using an overparameterized multilayer perceptron (MLP) via a novel nonparametric teaching perspective. The latter offers an efficient example selection framework for teaching nonparametrically defined (viz. non-closed-form) target functions, such as image functions defined by 2D grids of pixels. To address the costly training of INRs, we propose a paradigm called Implicit Neural Teaching (INT) that treats INR learning as a nonparametric teaching problem, where the given signal being fitted serves as the target function. The teacher then selects signal fragments for iterative training of the MLP to achieve fast convergence. By establishing a connection between MLP evolution through parameter-based gradient descent and that of function evolution through functional gradient descent in nonparametric teaching, we show for the first time that teaching an overparameterized MLP is consistent with teaching a nonparametric learner. This new discovery readily permits a convenient drop-in of nonparametric teaching algorithms to broadly enhance INR training efficiency, demonstrating 30%+ training time savings across various input modalities.
Overview Demos



Implicit Neural Teaching
In this paper, we commence by linking the evolution of an MLP that is based on parametric variation with the one that is perceived from a high-level standpoint of function variation. Next, by solving the formulation of MLP evolution as an ordinary differential equation (ODE), we obtain a deeper understanding of this evolution and the underlying cause for its slow convergence. Lastly, we introduce the greedy INT algorithm, which effectively selects examples with steeper gradients at an adaptive batch size and frequency.
Evolution of an overparameterized MLP
The evolution of an overparameterized MLP \( f_\theta \) can be converted into a differential form in a comparable manner: \begin{eqnarray} \frac{\partial f_{\theta^t}}{\partial t}= \underbrace{\left\langle\frac{\partial f(\theta^t)}{\partial \theta^t},\frac{\partial \theta^t}{\partial t}\right\rangle}_{(*)} + o\left(\frac{\partial \theta^t}{\partial t}\right). \end{eqnarray} By substituting the specific parameter evolution into the first-order approximation term \( (*) \) of the variational, we obtain \begin{eqnarray} \frac{\partial f_{\theta^t}}{\partial t}=-\frac{\eta}{N}\left[\left.\frac{\partial\mathcal{L}}{\partial f_{\theta}}\right|_{f_{\theta^t},\boldsymbol{x}_i}\right]^T_N\cdot\left[K_{\theta^t}(\boldsymbol{x}_i,\cdot)\right]_N+ o\left(\frac{\partial \theta^t}{\partial t}\right), \end{eqnarray} where the symmetric and positive definite neural tangent kernel (Jacot et al. 2018) \( K_{\theta^t}(\boldsymbol{x}_i,\cdot)=\left\langle\left.\frac{\partial f_{\theta}}{\partial \theta}\right|_{\cdot,\theta^t},\left.\frac{\partial f_{\theta}}{\partial \theta}\right|_{\boldsymbol{x}_i,\theta^t} \right\rangle \) Let the variational be expressed from a high-level standpoint of function variation. Using functional gradient descent, \begin{eqnarray} \frac{\partial f_{\theta^t}}{\partial t}=-\eta\mathcal{G}(\mathcal{L},f^*;f_{\theta^t},\{\boldsymbol{x}_i\}_N), \end{eqnarray} where the specific functional gradient is \begin{eqnarray} \mathcal{G}(\mathcal{L},f^*;f_{\theta^t},\{\boldsymbol{x}_i\}_N)=\frac{1}{N}\left[\left.\frac{\partial\mathcal{L}}{\partial f_{\theta}}\right|_{f_{\theta^t},\boldsymbol{x}_i}\right]^T_N\cdot \left[K({\boldsymbol{x}_i},\cdot)\right]_N. \end{eqnarray} The asymptotic relationship between NTK and the canonical kernel in functional gradient is presented in Theorem 1 below
Theorem 1
For a convex loss \( \mathcal{L} \) and a given training set \( \{(\boldsymbol{x}_i,y_i)|\boldsymbol{x}_i\in\mathcal{X},y_i\in\mathcal{Y}\}_N \), the dynamic NTK obtained through gradient descent on the parameters of an overparameterized MLP achieves point-wise convergence to the canonical kernel present in the dual functional gradient with respect to training examples, that is, \begin{eqnarray} \lim_{t\to\infty}K_{\theta^t}({\boldsymbol{x}_i},\cdot)=K({\boldsymbol{x}_i},\cdot), \forall i \in\mathbb{N}_N. \end{eqnarray}
It suggests that NTK serves as a dynamic substitute to the canonical kernel used in functional gradient descent, and the evolution of the MLP through parameter gradient descent aligns with that via functional gradient descent. Through this functional insight and the use of the canonical kernel (Dou & Liang, 2021) instead of NTK in conjunction with the remainder, it facilitates the derivation of sufficient reduction concerning \( \mathcal{L} \) in Proposition 2 below,
Proposition 2
Assuming that the convex loss \( \mathcal{L} \) is Lipschitz smooth with a constant \( \xi>0 \) and the canonical kernel is bounded above by a constant \( \zeta>0 \), if learning rate \( \eta \) satisfies \( \eta\leq1/(2\xi\zeta) \), then there exists a sufficient reduction in \( \mathcal{L} \) as \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial t}\leq -\frac{\eta\zeta}{2}\left(\frac{1}{N}\sum_{i=1}^N\left.\frac{\partial\mathcal{L}}{\partial f_{\theta}}\right|_{f_{\theta^t},\boldsymbol{x}_i}\right)^2. \end{eqnarray}
Spectral understanding of the evolution
Using the square loss \( \mathcal{L}(f_\theta(\boldsymbol{x}),f^*(\boldsymbol{x}))=\frac{1}{2}(f_\theta(\boldsymbol{x})-f^*(\boldsymbol{x}))^2 \) for illustration (Sitzmann et al., 2020; Tancik et al., 2020), one obtains the variational of \( f_\theta \) from a high-level functional viewpoint: \begin{eqnarray} \frac{\partial f_{\theta^t}}{\partial t}&=&-\eta\mathcal{G}(\mathcal{L},f^*;f_{\theta^t},\{\boldsymbol{x}_i\}_N)\nonumber\\ &=&-\frac{\eta}{N}\left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]^T_N\cdot \left[K(\boldsymbol{x}_i,\cdot)\right]_N. \end{eqnarray}
Solving this ODE, we obtain: \begin{eqnarray}\label{smode} \left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N=e^{-\eta\bar{\boldsymbol{K}}t}\cdot\left[f_{\theta^0}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N, \end{eqnarray} where \( \bar{\boldsymbol{K}}=\boldsymbol{K}/N \), and \( \boldsymbol{K} \) is a symmetric and positive definite matrix of size \( N\times N \) with entries \( K(\boldsymbol{x}_i,\boldsymbol{x}_j) \) at the \( i \)-th row and \( j \)-th column. Due to the symmetric and positive definite nature of \( \bar{\boldsymbol{K}} \), it can be orthogonally diagonalized as \( \bar{\boldsymbol{K}}=\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^T \) based on spectral theorem (Hall, 2013), where \( \boldsymbol{V}=[\boldsymbol{v}_1,\cdots,\boldsymbol{v}_N] \) with column vectors \( \boldsymbol{v}_i \) representing eigenvectors corresponding to eigenvalue \( \lambda_i \), and \( \boldsymbol{\Lambda}=\text{diag}(\lambda_1,\cdots,\lambda_N) \) is an ordered diagonal matrix (\( \lambda_1\geq\cdots\geq\lambda_N \)). Hence, we can express \( e^{-\eta\bar{\boldsymbol{K}}t} \) in a spectral decomposition form as: \begin{eqnarray} e^{-\eta\bar{\boldsymbol{K}}t}&=&\boldsymbol{I}-\eta t\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^T+\frac{1}{2!}\eta^2t^2(\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^T)^2+\cdots\nonumber\\ &=&\boldsymbol{V}e^{-\eta\boldsymbol{\Lambda} t}\boldsymbol{V}^T. \end{eqnarray} After rearrangement, the ODE solution can be reformulated as: \begin{eqnarray} \boldsymbol{V}^T\left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N=\boldsymbol{D^t}\boldsymbol{V}^T\left[f_{\theta^0}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N, \end{eqnarray} with a diagonal matrix \( \boldsymbol{D^t}=\text{diag}(e^{-\eta\lambda_1 t},\cdots,e^{-\eta\lambda_N t}) \). To be specific, \( \left[f_{\theta^0}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N \) refers to the difference vector between \( f_{\theta^0} \) and \( f^* \) at the initial time, which is evaluated at all training examples, whereas \( \left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N \) denotes the difference vector at time \( t \). Additionally, \( \boldsymbol{V}^T\left[f_{\theta^0}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N \) can be interpreted as the projection of the difference vector onto eigenvectors (i.e., the principal components) at the beginning, while \( \boldsymbol{V}^T\left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_N \) represents the projection at time \( t \). Figure below provides a lucid illustration in a 2D function coordinate system.
An illustration of the spectral understanding in a 2D function coordinate system (i.e., RKHS) with the \( \{K(\boldsymbol{x}_i,\cdot)\}_2 \) basis. The basis can be non-orthogonal if \( K(\boldsymbol{x}_i,\boldsymbol{x}_j)\neq0 \) for \( i\neq j \). The coordinate of \( f_{\theta^t}-f^* \) represents its projection on each axis, which is given by \( \langle\left(f_{\theta^t}-f^*\right),\left[K(\boldsymbol{x}_i,\cdot)\right]^T_2\rangle_{\mathcal{H}}=\left[f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]^T_2 \), and that of \( K(\boldsymbol{x}_\dagger,\cdot) \) is \( \langle K(\boldsymbol{x}_\dagger,\cdot),\left[K(\boldsymbol{x}_i,\cdot)\right]^T_2\rangle_{\mathcal{H}}=\left[K(\boldsymbol{x}_\dagger,\boldsymbol{x}_i)\right]^T_2 \), which is stored in the \( \dagger \)-th row of \( \boldsymbol{K} \). Assuming \( \bar{\boldsymbol{K}}=\left[\begin{array}{cc}
0.5 & 0.25 \\
0.25 & 0.5 \\
\end{array}\right] \), the eigenvalues and the respective eigenvectors can be computed as \( \lambda_1=0.75,\lambda_2=0.25 \) and \( \boldsymbol{v}_1=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})^T,\boldsymbol{v}_2=(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})^T \), respectively. Assuming \( [f_{\theta^t}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)]_2 \) equals \( (1,0.5) \), its first and second principal component projections are \( \frac{3\sqrt{2}}{4} \) and \( -\frac{\sqrt{2}}{4} \), respectively. Moreover, the discrepancy between \( f_{\theta^t} \) and \( f^* \) diminishes at a rate of \( e^{-\frac{3\eta t}{4}} \) and \( e^{-\frac{\eta t}{4}} \) for the first and second principal components, respectively.
Based on the above, it reveals the connection between the training set and the convergence of \( f_{\theta^0} \) towards \( f^* \), which indicates that when evaluated on the training set, the discrepancy between \( f_{\theta^0} \) and \( f^* \) at the \( i \)-th component exponentially converges to zero at a rate of \( e^{-\eta\lambda_i t} \), which is also dependent on the training set (Jacot et al. 2018). Meanwhile, this insight uncovers the reason for the sluggish convergence that empirically arises after training for an extended period, wherein small eigenvalues hinder the speed of convergence when continuously training on a static training set.
INT algorithm
With the spectral analysis above, a deeper understanding of INT follows. First, we define the entire space as the one spanned by the basis corresponding to the whole training set \( \{K(\boldsymbol{x}_i,\cdot)\}_N \). Similarly, \( \{K(\boldsymbol{x}_i,\cdot)\}_k\subseteq\{K(\boldsymbol{x}_i,\cdot)\}_N \) spans subspaces associated with the selected examples. The eigenvalue of the transformation from the entire space to the subspace of concern (i.e., spanned by \( \{K(\boldsymbol{x}_i,\cdot)\}_k \) associated with selected examples) is one, while it is zero for the subspace without interest (Watanabe & Katagiri, 1995; Burgess & Van Veen, 1996). The spectral understanding indicates that \( f_{\theta^t} \) approaches \( f^* \) swiftly at the early stage within the current subspace, owing to the large eigenvalues (Jacot et al. 2018). Hence, the INT algorithm can be interpreted as dynamically altering the subspace of interest to fully exploit the period when \( f_{\theta^t} \) approaches \( f^* \) rapidly. Meanwhile, by selecting examples based on \begin{eqnarray} {\{\boldsymbol{x}_i\}_k}^*=\underset{\{\boldsymbol{x}_i\}_k\subseteq\{\boldsymbol{x}_i\}_N}{\arg\max}\left\|\left[f_{\theta}(\boldsymbol{x}_i)-f^*(\boldsymbol{x}_i)\right]_k\right\|_2, \end{eqnarray} the subspace of interest is precisely the one where \( f_{\theta^t} \) remains significantly distant from \( f^* \). In a nutshell, the INT algorithm, by dynamically altering the subspace of interest, not only maximizes the benefits of the fast convergence stage but also updates \( f_{\theta^t} \) in the most urgent direction towards \( f^* \), thereby saving computational resources compared to training on the entire dataset.
Experiments and Implementations
We provide a plug-and-play package to generally speed up INRs training.
Toy 2D Cameraman fitting.
Reconstruction quality of SIREN. (b) trains SIREN without (w/o) INT using all pixels. (c) trains it w/o INT using 20% randomly selected pixels. (d) trains it using INT of 20% selection rate. (e) trains it using progressive INT (i.e., increasing selection rate progressively from 20% to 100%).
Progression of INT selected pixels (marked as black) at corresponding iterations when training with INT 20% (top) and 40% (bottom).
INT on multiple real-world modalities.
| INT | Modality | Time (s) | PSNR(dB) / IoU(%) ↑ |
|---|---|---|---|
| ✗ | Audio | 23.05 | 48.38 ± 3.50 |
| Image | 345.22 | 36.09 ± 2.51 | |
| Megapixel | 16.78K | 31.82 | |
| 3D Shape | 144.58 | 97.07 ± 0.84 | |
| ✓ | Audio | 15.76 (-31.63%) | 48.15 ± 3.39 |
| Image | 211.04 (-38.88%) | 36.97 ± 3.59 | |
| Megapixel | 11.87K (-29.26%) | 33.01 | |
| 3D Shape | 93.19 (-35.54%) | 96.68 ± 0.83 |
Signal fitting results for different data modalities. The encoding time is measured excluding data I/O latency.
Related links
Related works (for developing a deeper understanding of INT) are:
[NeurIPS 2023] Nonparametric Teaching for Multiple Learners,
[ICML 2023] Nonparametric Iterative Machine Teaching.
You can find the datasets used in this project here: Cameraman, Kodak, Pluto image, Stanford 3D Scanning Repository dataset.
Citation
Acknowledgements
We thank all anonymous reviewers for their constructive feedback to improve this project.
This work was supported by the Theme-based Research Scheme (TRS) project T45-701/22-R, and in part by ACCESS – AI Chip Center for Emerging Smart Systems, sponsored by InnoHK funding, Hong Kong SAR.
The website template was borrowed from Michaël Gharbi.
Send feedback and questions to Chen Zhang